One question type that appears frequently on both SAT Math sections (no calculator and calculator) is the systems of equations question type. This question type gives you two different equations with two different variables and asks you to solve for one or more of the variables. In general, students tend to struggle at the very beginning or very end of the systems of equations solving process. Either they won’t know how to get started or they’ll rush too quickly and fall for a trap answer. Here are some foolproof steps to help you solve SAT systems of equations questions on test day.
Step One: Determine What You’re Solving For
There are a wide variety of systems of equations SAT Math questions. Some simply ask you to solve for a variable, while others ask you to solve a computation between variables or to find values that meet a specific condition. Because your objective will change based on the individual question, it’s important to be attentive to exactly what you need to solve for. Take the following two questions, for example.
Question One:
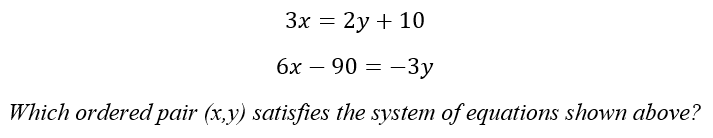
Question Two:
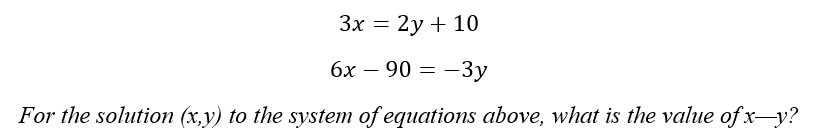
Although both of the above questions refer to the same system of equations, they require us to solve in different ways. In the first question, we must simply solve for x and y. In the second question, however, we must go one step further by solving for the difference between x and y.
Step Two: Line Up Your Equations
Always start by putting all variables on the left side of the equation and all constants on the right. This will allow you to line up and solve your system.
Equation One:
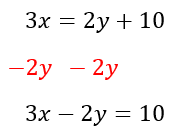
Equation Two:
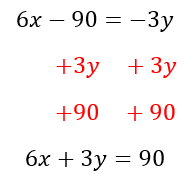
Resulting System:
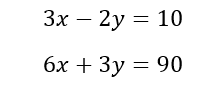
Step Three: Solve Using Elimination or Substitution
Next, decide if you’ll use elimination or substitution. If you can easily transform the system so that one set of corresponding coefficients “cancels out” when you add or subtract the equations, elimination is usually the more efficient method. If you don’t see a quick and easy way to make elimination work, you can always use substitution. We’ll look at both methods using the following system of equations:
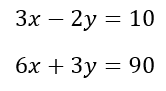
Elimination:
In the above system of equations. I can multiply the first equation by 2 and then cancel the x’s to solve for y I can then plug my y back into either equation to solve for x.
Step One: Multiply one equation by a coefficient.
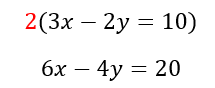
Step Two: Cancel out one variable.
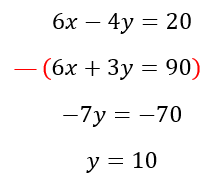
Step Three: Solve for the other variable.
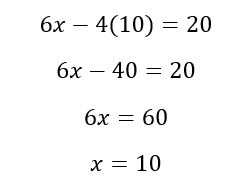
Substitution:
Another way to solve systems of equations is through substitution. Some students prefer substitution because it does not require as much advanced planning. However, it can also result in messier math, so we usually advise it as a last resort. To use substitution, solve for one of your variables and plug your result back into the other equation.
Step One: Isolate for x in one equation
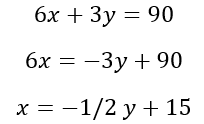
Step Two: Plug in for x in other equation
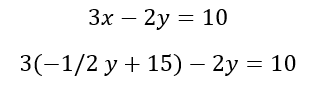
Step Three: Solve for y
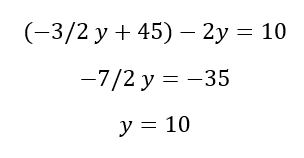
Step Four: Solve for x
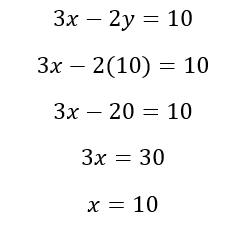
Step Four: Watch Out For Trap Answers!
By now, we know to never answer hastily on the SAT, and systems of equations are no exception. Once you solve your system, don’t just circle the first answer choice that appears to match. The SAT loves to trick us by including answer choices that match some of the math we’ve done, but not all. Instead, look back at your question and remind yourself what you’re solving for. Is it a solution set? A variable? A coefficient? Only after confirming exactly what you need should you answer the question.
Let’s try a sample question using our multi-step approach:
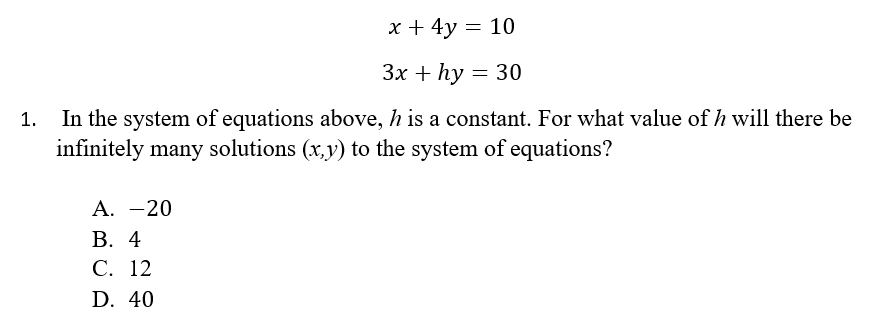
First, let’s identify what we’re solving for. The question asks us to find a value of h for which infinitely many solutions between the two equations exist. We know that “infinitely many” solutions occur when two equations are equal to one another. Therefore, we need to find a value of h that makes my given equations equal.
Next, let’s decide which method—elimination or substitution—to use. In this case, it looks like we can easily multiply the first equation by three to eliminate the x’s, so we’ll use elimination.
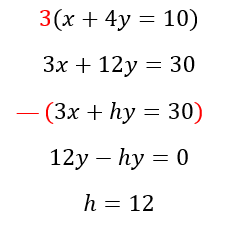
Since a value of 12 allows for infinitely many solutions to the given equations, the answer is C.
But just for fun, let’s look at how the other answer choices are designed to trick us. Answer A might look attractive because it’s the difference between 10 and 30. If I had subtracted the two equations without further manipulation, this is the answer I would have gotten. Similarly, I would get D if I added. Finally, notice answer choice B matches the coefficient in the first equation. This is intentional. The test-makers know that students will be looking to make the two equations equivalent and may therefore jump at an equivalent coefficient.
SAT systems of equations questions certainly require care and precision to be solved correctly. However, with ample practice and an eye for detail, you can undoubtedly master this question type on test day!

