Continuing in our discussion of common student weaknesses on the ACT Math section, today we turn our attention to trigonometry questions. Trigonometry questions can span any difficulty level on the ACT, but they tend to be on the more difficult side. Before trying the hardest trigonometry questions, check out our blog about how to identify relevant geometry equations on the ACT.
As we did in last week’s blog, we will start today with three simple definitions: sine (sin), cosine (cos), and tangent (tan). These three functions form the basis of all ACT trigonometry problems and draw their definitions from right triangles. To remember the definitions of sin, cos, and tan, rely on this acronym: SohCahToa. This acronym results in the following definitions:
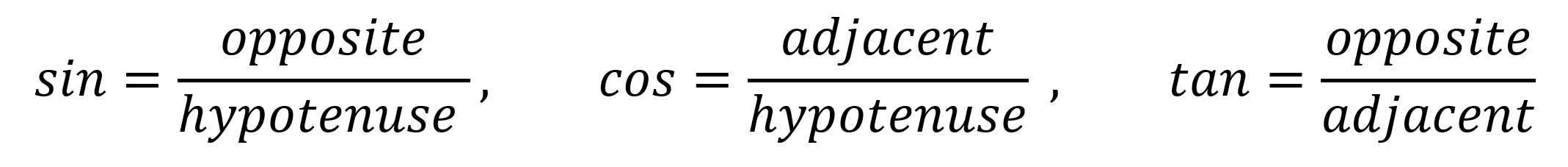
Let’s take a look at an example of how to apply these definitions with a sample triangle.
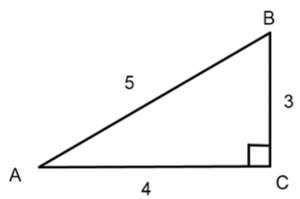
Focusing on angle A, the side length to the opposite of it is 3. The hypotenuse is 5. That means that sin(A)=3/5. Take a second to practice this technique by finding the cos(A) and tan(A).
Another way that the ACT frequently tests trigonometry is by combining these three trig functions with the Pythagorean theorem. Let’s take a look at an example of one of the harder ACT trig functions:
In a right triangle ABC, the sine of A is 8/17. What is the tangent of B?
At first, this problem may seem impossible, as there is simply not enough information to solve it. But let’s use the diagram of a right triangle that we had before and label it with as much information as possible. If the sine of angle A is 8/17, use SohCahToa to label two sides of the triangle. Label any unknown side with a variable. You should end up with this:
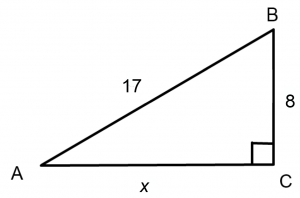
Now, apply the Pythagorean theorem:
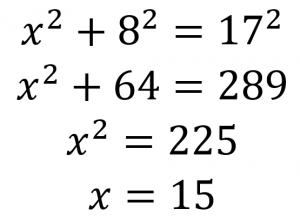
All of a sudden our figure is looking much more complete! Applying SohCahToa again, we can see that tan(B) = 15/8.
As always, when completing an ACT geometry question, we want to add as much information as possible to the figure. Once you’ve done that, rely on SohCahToa and the Pythagorean theorem to take you through the steps to find the answer.
Related Posts
How To: Identify Relevant Geometry Equations
How To: Answer Statistics Questions

